Research
My current research interests lie in the intersection of the following areas: (1) scientific machine learning and data-driven methods, (2) computational inverse and ill-posed problems, and (3) numerical methods for partial differential equations.
Full publication list: see publications
Selected research highlights:
Element learning: a systematic approach of accelerating finite element-type methods via machine learning
My research interests in this area center around the consideration of the following two closely related questions:
1. What are the advantages and limitations of machine learning based methods compared to
classical numerical methods (e.g. finite
element)?
2. How to combine their advantages?
Thinking about the above two questions has led to a recent discovery of a new computational framework which we call element learning. This new approach can be used to systematically accelerate finite element-type methods through machine learning while still retaining the many advantages of classical finite element-type methods, such as proficient handling of complex geometry and boundary conditions, reliability, etc.
See the following figures for one of our numerical results and a visual explanation of the core idea of element learning.
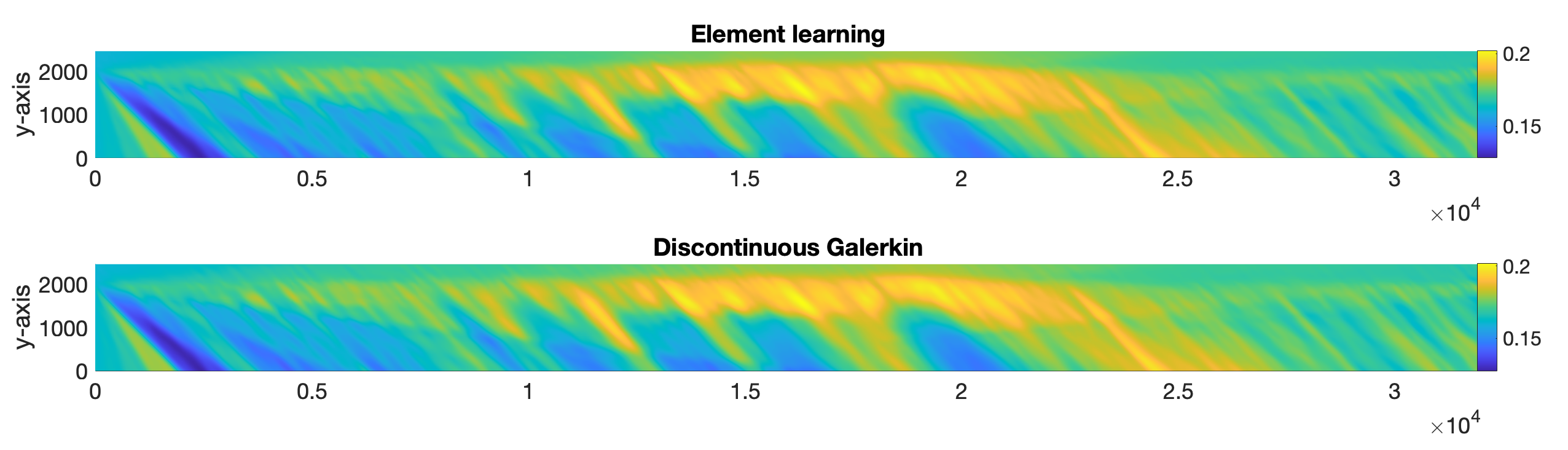
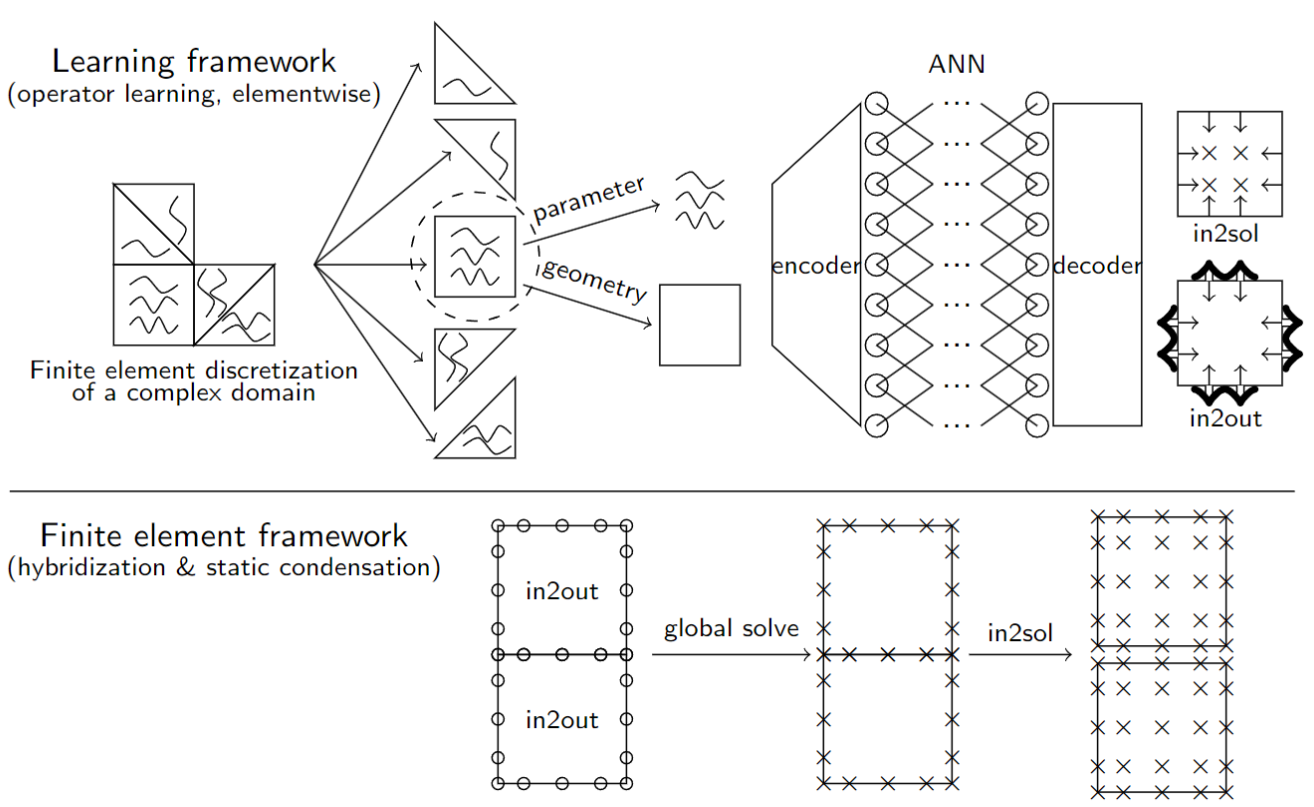
- S. Du, and S. N. Stechmann. Element learning: a systematic approach of accelerating finite element-type methods via machine learning, with applications to radiative transfer.
J. Comput. Math. (2024). DOI: 10.4208/jcm.2407-m2024-0047
Adaptive-mesh inversion: a goal-oriented hp-adaptive mesh refinement method for solving inverse radiative transfer problem
Inverse radiative transfer serves as the mathematical foundation for a wide spectrum of applications such as optical tomography and remote sensing. Despite its broad applications, devising numerical methods for inverse radiative transfer is notoriously challenging due to the high-dimensional nature of the forward problem. Standard discretizations that meet the accuracy standards often demand significant memory resources, making the solver inefficient and sometimes impractical. This challenge amplifies in the inverse problem scenario, where numerous iterations of the forward problems are necessary. As such, there's a pressing need to design numerical methods that are memory-efficient and have fewer degrees of freedom (DOFs) without compromising on accuracy.
To address the challenges previously mentioned, we introduced the so called adaptive-mesh inversion method. This is a goal-oriented hp-adaptive mesh refinement (AMR) technique tailored for solving inverse problems. A distinctive feature of the approach is the integration of two optimization processes: one for inversion and the other for mesh adaptivity. By leveraging the connections between duality-based mesh adaptivity and adjoint-based inversion techniques, we are able to devise a goal-oriented error estimator. This estimator is cost effective to compute. The numerical tests suggest it can efficiently steer mesh-refinement to effectively address the inverse radiative transfer problem. The main idea of the methodology can be visually represented as in the following figure.

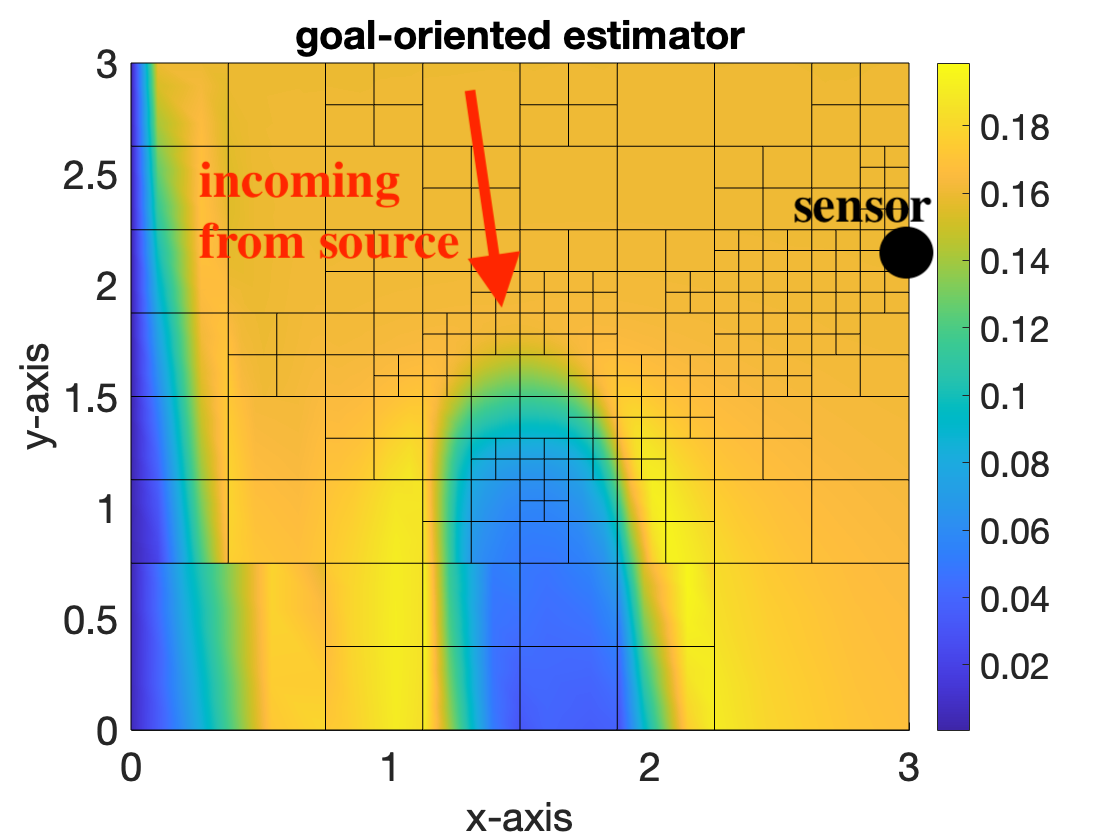
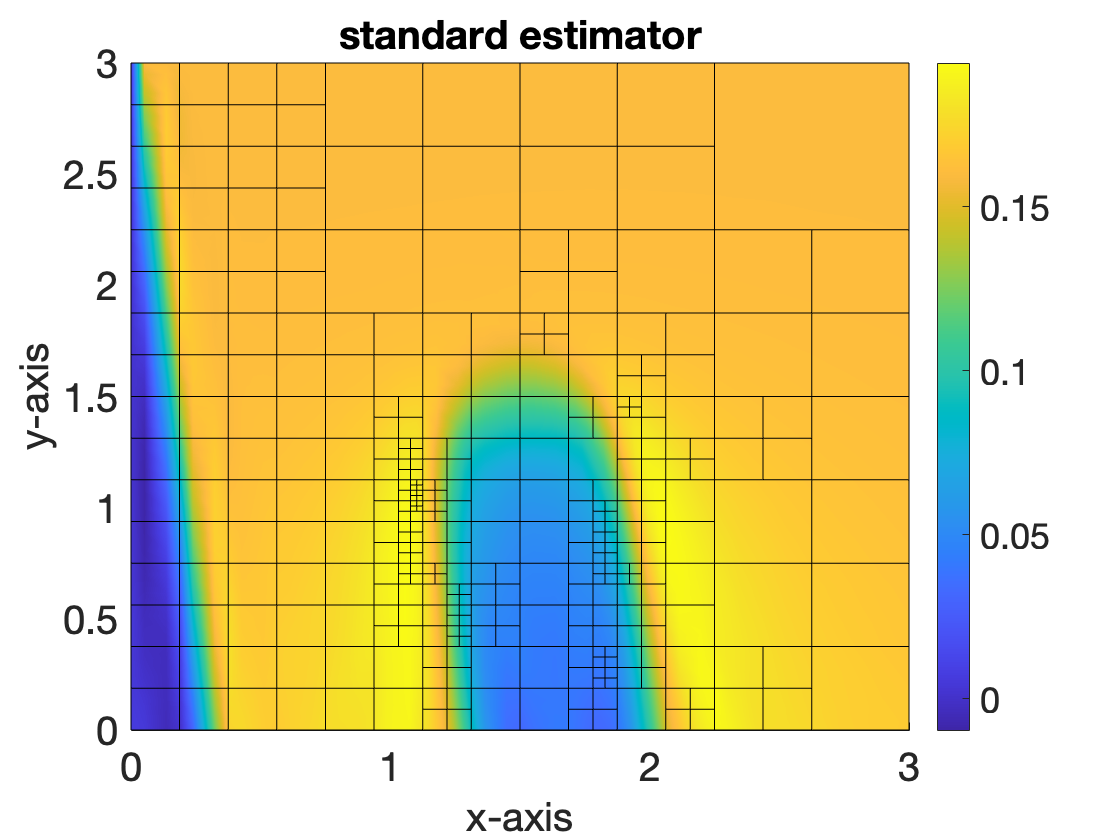
- S. Du, and S. N. Stechmann. Inverse radiative transfer with goal-oriented hp-adaptive mesh refinement: adaptive-mesh inversion.
Inverse Probl. 39 (2023), no. 11. DOI: 10.1088/1361-6420/acf785 - S. Du, and S. N. Stechmann. Fast, low-memory numerical methods for radiative transfer via hp-adaptive mesh refinement.
J. Comput. Phys. 480 (2023). DOI: 10.1016/j.jcp.2023.112021
Symplectic Hamiltonian finite element methods for electromagnetics
Symplectic Hamiltonian finite element methods (SHFEM) are a special type of numerical methods for numerically approximating the solution of Hamiltonian partial differential equations. These methods use Galerkin space-discretizations which result in a system of ODEs displaying a discrete version of the Hamiltonian structure of the original system. The resulting system of ODEs is then discretized by a symplectic time-marching method. This combination results in high-order accurate, fully discrete methods which can preserve the invariants of the Hamiltonian defining the ODE system. The following figure shows an example with electromagnetics waves propogating in a non-homogeneous medium. It shows that our SHFEM method conserves the energy of the semidiscretization in space up to 10 digits of precision, and does not allow the exact energy to drift in time.
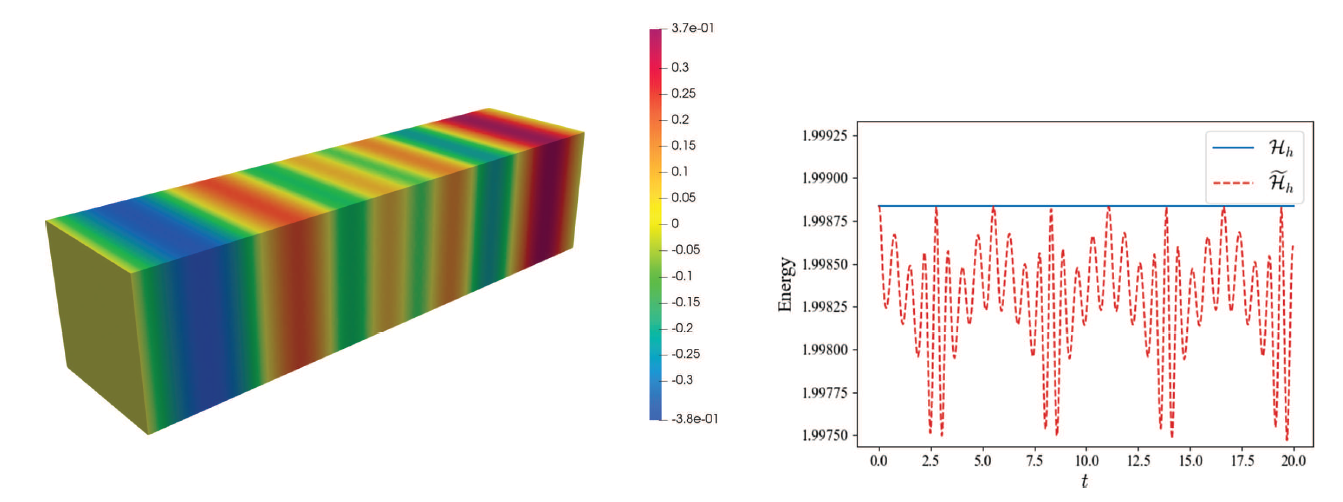
- B. Cockburn, S. Du, and M. A. Sánchez. A priori error analysis of new semidiscrete, Hamiltonian HDG methods for the time-dependent Maxwell's equations.
ESAIM: M2AN, 57 (2023), no.4, 2097 – 2129. DOI: 10.1051/m2an/2023048 - B. Cockburn, S. Du, and M. A. Sánchez. Combining finite element space-discretization with symplectic time-marching schemes for linear hamiltonian systems.
Front. Appl. Math. Stat. 9 (2023). DOI: 10.3389/fams.2023.1165371 - M. A. Sánchez, S. Du, B. Cockburn, N.-C. Nguyen, J. Peraire. Symplectic Hamiltonian finite element methods for electromagnetics.
Comput. Methods Appl. Mech. Engrg. 396 (2022). DOI: 10.1016/j.cma.2022.114969 - B. Cockburn, M. A. Sánchez, S. Du. Discontinuous Galerkin methods with time-operators in their numerical traces for time-dependent electromagnetics.
Comput. Meth. Appl. Math. 22 (2022), no. 4, 775-796. DOI: 10.1515/cmam-2021-0215
Generalized projection-based analysis of hybridizable discontinuous Galerkin methods
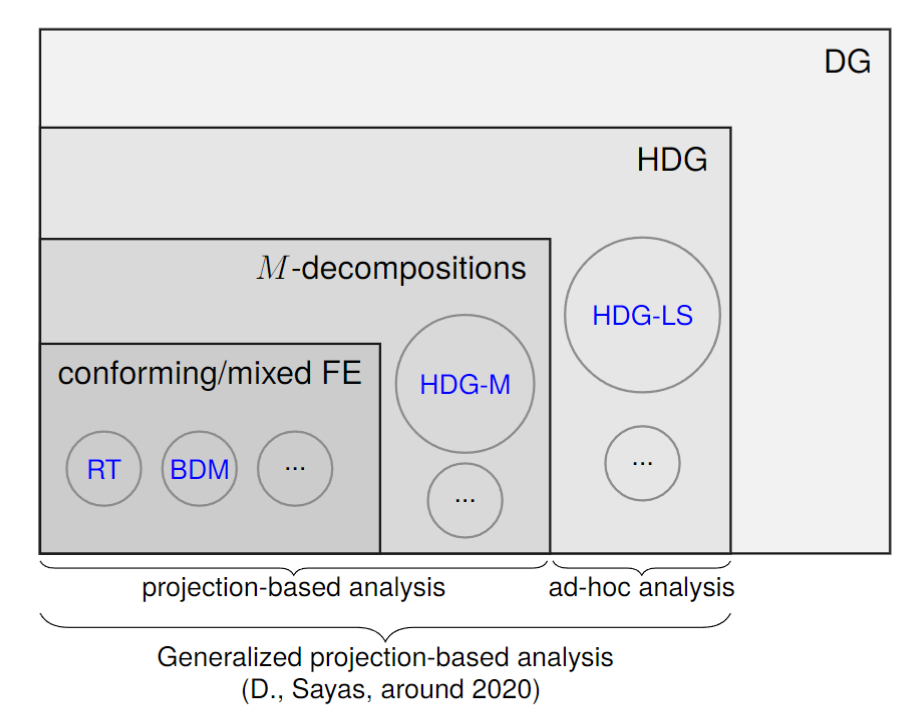
Hybridizable discontinuous Galerkin methods (HDG) lie in between the two most important groups of finite element-type methods: (1) conforming/mixed methods and (2) discontinuous Galerkin (DG) methods. This enables HDG to combine the many advantages from these two groups.
Despite the many advantages of HDG methods, their analysis was also separated into two groups: for those more alike mixed methods, they were analyzed similar to the classical analysis of mixed methods, by the so-called projection-based analysis; on the other hands, for those more alike nonconforming/DG methods, they were analyzed by ad-hoc approaches. This separation of analysis has several undesired consequences: (1) Those ad-hoc analysis is not as concise and simple as the projection-based analysis, (2) Ad-hoc analysis becomes difficult for complicated problems (e.g., time-dependent problems, coupling problems), (3) Analysis is hard to reuse because of the separation.
To address this issue, we developed the so-called generalized projection-based analysis, extending the classical projection-based analysis to those HDG method which do not admit M-decomposition (e.g. Lehrenfeld-Schoberl HDG), thus enabling a unified analysis. With these new analysis tools, we are able to devise/analyze new HDG methods or improve the analysis of existing ones. The applications include time-harmonic and transient elastic waves, static and time-dependent Maxwell’s equations and Stokes equations.
- B. Cockburn, S. Du, and M. A. Sánchez. A priori error analysis of new semidiscrete, Hamiltonian HDG methods for the time-dependent Maxwell's equations.
ESAIM: M2AN, 57 (2023), no.4, 2097 – 2129. DOI: 10.1051/m2an/2023048 - S. Du, and F.-J. Sayas. A note on devising HDG+ projections on polyhedral elements.
Math. Comp. 90 (2021), 65-79. DOI: 10.1090/mcom/3573 - S. Du. HDG methods for the Stokes equation based on strong symmetric stress formulations.
J. Sci. Comput. 85, 8 (2020). DOI: 10.1007/s10915-020-01309-7 - S. Du, and F.-J. Sayas. A unified error analysis of hybridizable discontinuous Galerkin methods for the static Maxwell equations.
SIAM J. Numer. Anal. 58 (2020), no. 2, 1367–1391. DOI: 10.1137/19M1290966 - S. Du, and F.-J. Sayas. New analytical tools for HDG in elasticity, with applications to elastodynamics.
Math. Comp. 89 (2020), 1745-1782. DOI: 10.1090/mcom/3499